前言
本文内容主要摘自《分布式系统原理与范型》,主要用于本人后续回顾学习用,建议阅读原书。
关于时钟
几乎所有的计算机都有一个计时电路,我们一般会称这个计时电路为「时钟」(但它们并不是通常意义上的时钟,我们将其称为「计时器」可能会更恰当一些)。「时钟」与进程之间的协作和同步有密切的关系,多个进程之间是通过「事件」发生的「时间」来就「事件」的发生顺序达成一致的。在单机单时钟的情况下,如果这个时钟存在少许偏差是不会出现问题的,因为这台机器上的所有进程都使用同一个时钟,所以它们的内部仍然会保持一致。
逻辑时钟
在许多应用中,只要所有的机器能维持一个全局统一的时间就够了,这个时间并不需要与真实时间一致。对于某类算法而言,重要的是时钟的内部一致性,而不是它们是否与真实时间接近。这类算法通常将时钟称为「逻辑时钟」(logical clock)。
Lamport在其著名的论文「Time, Clocks, and the Ordering of Events in a Distributed System 」中阐明了「尽管时钟同步是可能的,但它不是绝对必要」的观点。如果两个进程不进行交互,那么他们的时钟也无须同步,这是因为即使没有进行同步也察觉不出来,并且也不会产生问题。他指出,通常重要的不是所有的进程在时间上完全一致,而是它们在事件的发生顺序上要达成一致。
Lamport时间戳
为了同步逻辑时钟,Lamport定义了一个称为「先发生」(happens-before)的关系。表达式$a \rightarrow b$读作「a在b之前发生」,意思是所有进程一致认为事件a先发生,然后事件b才发生。这种「先发生」关系有两种情况:
- 如果a和b是同一个进程中的两个事件,且a在b之前发生,则$a \rightarrow b$为真;
- 如果a是一个进程发送消息的事件,而b为另一个进程接受该消息的事件,则$a \rightarrow b$也为真。消息不可能在发送之前就被接受,也不可能在发送的同时被接受,这是因为消息需要一定时间才能到达接收端。
「先发生」关系是一种传递关系,所以如果$a \rightarrow b$且$b \rightarrow c$,则有$a \rightarrow c$。如果事件x和y发生在两个互不交换消息的进程中(也不通过第三方间接交换消息),那么无论是$x \rightarrow y$还是$y \rightarrow x$都不为真。这两个事件被称为「并发的」(concurrent),这意味着无法说或者不必说这两个事件什么时候发生,哪个事件先发生。
我们需要一种测量事件的方法,使得对于每个事件a,我们都能为它分配一个所有进程都认可的时间值$C(a)$。同时这些时间值必须具有如下性质:
如果$a \rightarrow b$,那么$C(a) < C(b)$;
时钟时间值$C$必须总是前进(增加),不能倒退(减少),校正时间的方法是给时间加上一个正值而不是减去一个正值;
如下图所示,三个进程运行在不同的机器上,每个机器以各自的速率工作。当进程A的时钟「滴答」了6次时,进程B的时钟「滴答」了8次,进程C的时钟「滴答」了10次。我们下面描述一个从进程A到B再到C的消息传递及响应过程:
在0时刻,进程A将消息a发送给进程B,消息的传输时间取决于信任哪个时钟。不管怎样,当它到达进程B时,进程B的时钟为16。如果消息a上携带了其在进程A上打包的时钟值0,则进程B会推算其传输时间为$16 - 0 = 16$个时钟值。
进程B在其时钟值为24时,将消息b发送给进程C,在进程C的时钟值为40时到达进程C。
进程C在其时钟值为50时,将响应消息c发送给进程B,在进程B的时钟值为48时到达进程B。
进程B在其时钟值为56时,将响应消息d发送给进程A,在进程A的时钟值为54时到达进程A。
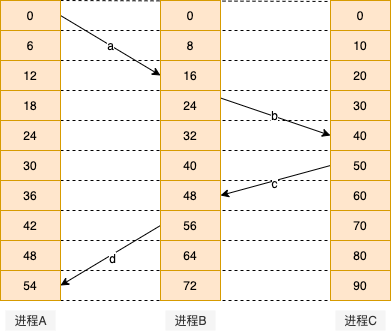
分析以上过程,我们可以发现一个有意思的现象,响应消息从进程C时钟值为50时刻出发,却在进程B时钟值为48时刻到达进程B,响应消息d也有类似的现象——消息的到达时刻竟然比消息的发送时刻还要早,这显然是不合理的,必须避免这种情况发生。
Lamport给出的解决方案是直接遵循「先发生关系」。消息c在时钟值为50时离开,那么它只能在时钟值为51或更晚时到达。所以每个消息都应该携带发送者时钟的「发送时间」。当消息到达,并且接受者时钟显示的时间值比消息的发送时间早时,接受者就把它的时钟调到一个比发送时间大1的值。调整后的过程图如下所示。
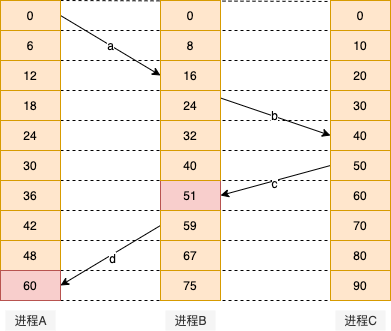
对这个算法稍作补充就可以满足全局时间的需要,即在每两个事件之间,时钟必须至少「滴答」一次。如果一个进程以相当快的速度连续发送或接收两个消息,那么它的时钟必须在这之间至少「滴答」一次。
在某些情况下还需要一个附加条件,即两个事件不会精确的同时发生。为了达到这个目标,我们可以将事件发生的进程号附加在时间的低位后,并用小数点分隔开。使用这种方法,如果进程1和进程2同时在40时刻发生了一个事件,那么前者可以标记为「40.1」,后者可以标记为「40.2」。
通过使用这种方法,我们现在有了一个为分布式系统中的所有事件分配时间的方法,这遵循下面的规则:
- 若在同一进程中a在b之前发生,则$C(a)<C(b)$;
- 若a和b分别代表发送一个消息和接受该消息的事件,则C(a)<C(b);
- 对于所有不同的事件a和b,$C(a) \neq C(b)$;
这个算法为我们提供了一种对系统中所有的事件进行完全排序的方法。许多其他的分布式算法都需要这种排序以避免混淆,所以此算法在各种文献被广泛引用。
向量时间戳
Lamport时间戳导致分布式系统中的所有事件都要经过排序以具有这样的性质:如果事件a发生在事件b之前,那么a也应该排在b之前,即$C(a) < C(b)$。
然而,使用Lamport时间戳后,只通过比较事件a和b各自的时间值$C(a)$和$C(b)$,无法说明它们之间的关系。换句话说,$C(a) < C(b)$不能说明事件a就是在事件b之前发生的。问题在于Lamport时间戳不能捕获因果关系(causality)。
因果关系可以通过向量时间戳(Vector Timestamp)来捕获。分配给事件a的**向量时间戳 $VT(a)$**具有下列性质:如果对于某一事件b,有 $VT(a) < VT(b)$,那么认为事件a在因果关系上处于事件b之前。
向量时间戳的创建是通过让**每个进程$P_n$维护一个向量$V_n$**来实现的,该向量具有下面两个性质:
- $V_i[i]$是到目前为止进程$P_i$发生的事件的数量;
- 如果$V_i[j] = k$,那么进程$P_i$知道进程$P_j$中已经发生了$k$个事件;
第一个性质是通过在**进程$P_i$中的新事件发生时递增$V_i[i]$**来维护的。
第二个性质是通过在所发送的消息中携带向量时间戳来维护的,当进程$P_i$发送消息$m$时,它将自己的当前向量作为时间戳$vt(m)$一起发送。
通过使用这种方式,接受者可以得知进程$P_i$中已经发生的事件数。更重要的是,接受者可以得知在进程$P_i$发送消息$m$之前其他进程已经发生了多少个事件。换句话说,消息$m$的时间戳$vt(m)$告诉接受者其他进程中有多少事件发生在消息$m$之前,并且$m$可能在因果关系上依赖于这些事件。
进程$P_j$依赖于其接收到的消息来调整自己所维护的向量。当进程$P_j$在接收到消息$m$时,它调整自己的向量,将每项$V_j[k]$设置为$max{V_j[k], vt(m)[k]}$。该向量现在反映了进程$P_j$所必须接受到消息数目,该消息数目至少是在发送$m$之前见到的消息。此后将$V_j[i]$增1,这表示接受消息$m$的事件是来自于进程$P_i$的下一个事件。
只在不违背因果关系限制时,才能使用向量时间戳来传递消息。
示例:
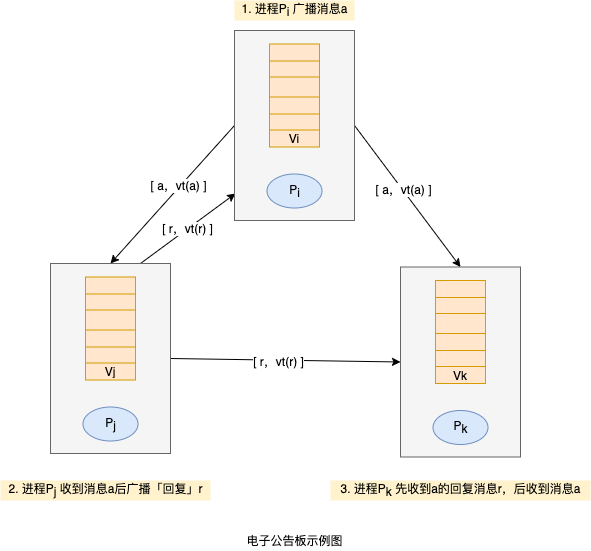
我们来考虑一个电子公告板的例子。当进程$P_i$张贴一篇文章时,它将改文章作为消息$a$广播出去,并且在该消息上附加一个时间戳$vt(a)$,其值等于$V_i$。当另一个进程$P_j$接收到消息$a$时,它将根据其携带的时间戳$vt(a)$来调整自己的向量,以使$V_j[i] > vt(a)[i]$。
假设进程$P_j$在收到消息$a$后广播了一个该文章的回复消息$r$,消息$r$携带值等于$V_j$的时间戳$vt(r)$。需要注意的是$vt(r)[i] > vt(a)[i]$。假设通信是可靠的,包含文章的消息$a$和包含回复的消息$r$最终都到达了另一个进程$P_k$。
因为我们没有对消息的顺序关系做出假设,所以消息$r$可能在消息$a$之前到达进程$P_k$。进程$P_k$接受到消息$r$时检查其时间戳,并决定推迟提交消息$r$,直到因果关系上位于$r$之前的消息都接受到了才提交$r$。消息$r$ 只有在满足下列条件时才得到交付:
- $vt(r)[j] = V_k[j] + 1$;
- 对于所有满足$i \neq j$的$i$和$j$,$vt(r)[i] < V_k[i]$;
第一个条件说明$r$是进程$P_k$正在等待的下一条来自进程$P_j$的消息;
第二个条件说明当进程$P_j$发送消息$r$时,进程$P_k$只看到被进程$P_j$看到的消息。这意味着进程$P_k$已经看到了消息$a$。