AC-Key:Adaptive Caching for LSM-based Key-Value Stores
2023-12-18 21:59:30 # 论文 #Key-Value #Store #论文阅读

0x00 Introduction

大多数现有的KVS都采用了Log-Structured Merge(LSM) tree来提高写操作的性能，然而LSM的结构特性使得读操作的性能受到了很大的影响。当在多个Level中查找一个key时会引起多次磁盘的I/O操作，带来较大的性能开销。
而大部分工作负载都有访问局部性的特征，缓存便是利用这一特性来提高读操作性能的主要技术。针对企业级工作负载的研究发现，无论是「point lookup」还是「range query」都展现出了「hot spots」的现象。
因此，为基于LSM的KV-Store设计高性能的缓存方案主要有两个技术挑战：

  • 首先，LSM分层的设计使得缓存不同Level的KV数据所带来的收益不同，也即能够节省的磁盘I/O次数不同；
  • 其次，两种读操作「point lookup」和「range query」对缓存的需求不一致。「Point lookup」更偏向于缓存一个「key-value pair」，这种方式相对节省空间；当value过大时，一种折中的方案是选择缓存「key- pointer pair」，也即缓存「key」和「value的磁盘指针」，指针相对value所占用的空间更小。而缓存单个零星的「key-value pair」无法为「range query」服务，因此只能通过缓存「block」来支持「range query」；

因此，很难在缓存KV、KP和Block之间进行权衡，它们都有其各自适合的工作负载。此外，设计一种可以根据工作负载进行自适应的缓存方案是困难的。
现有的缓存方案通常只选择缓存KV、KP和Block中的一种或两种，而且为每种缓存类型都分配了固定大小的缓存空间。因此，这些缓存方案无法适应多样的工作负载，也不能根据工作负载的变化来调整缓存空间的大小。此外，目前还没有针对LSM中特有的异构缓存成本的解决方案。
本文全面分析研究了对缓存KV、KP和Block之间的权衡，并提出了「 AC-Key, Adaptive Caching for LSM-based Key-Value Stores」来结合它们在面临各种工作负载时的优势。AC-Key为每种类型的条目（KV、KP和Block）都使用专门设计的单独缓存组件。每个缓存组件的大小可以根据文章提出的「 hierarchical adaptive caching algorithm，分层自适应缓存算法」进行调整（使用「ghost cache」来指导其大小调整）。
此外，AC- Key利用一种新颖的缓存效率因子来评估不同的缓存成本和收益，以指导不同缓存组件之间的边界调整以及缓存组件内部的替换策略。

0x11 LSM-Tree-Based Key-Value Store

基于LSM tree的Key-Value store（LSM- KVS）的流行实现，例如LevelDB和RocksDB，都由两部分组成：

  • Memory Component，或者说MemTable，通常使用原地排序（in-place sorted）的数据结构来实现，例如「skip-list」或「$B^+$ tree」；
  • Storage Component，通常被实现为存储有序run（压缩的Key-Value对组成）的多层文件；

如图1所示，每个Level被划分为多个「sorted string table files」也即SSTs，每个SST都有配置的大小限制，通常为2MB～64MB。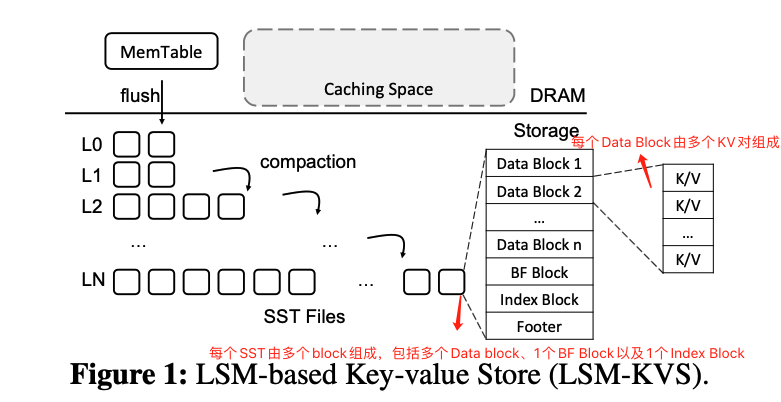
image-20211210110007408

除了$L_0$之外，每个Level都是一个单独的有序run，其中，SST之间具有不相交的key范围。在有序run中，一个SST的所有key-value对被划分到多个数据块（data block）中。SST中每两个相邻数据块之间的边界key存储在索引数据块（index block）中，索引数据块在SST中有相应的数据块偏移量（data block offset）。此外，每个SST还包含一个「bloom filter block」（BF block，布隆过滤块）来确定SST中是否存在某个key，以避免不必要的磁盘I/O操作。「Block」是LSM- KVS中的基本磁盘I/O单元。
在LSM-KVS中有两种类型的读操作，分别是「point-lookup」（也即Get）和「range query」（也即Scan）。Get按照下面的顺序来查找指定key的value：先是检查内存中的MemTable，然后是磁盘上$L_0$中从新到旧的每个SST，$L_0$中查找失败则继续查找$L_1$~$L_N$。
如果在内存MemTable中就找到了要找的key，则不需要任何的磁盘访问就可以返回相应的value。否则，则需要在磁盘组件中查询SST文件。查询SST时会先检查对应的布隆过滤器，如果布隆过滤器指示该SST不存在指定key的话则跳过此SST。反之，则读取索引块来定位key所在的具体数据块，最后读取相应数据块来查找此key。因此，在一个SST中查找一个key最多需要三次磁盘I/O操作：

  • 第一次读Bloom filter block；
  • 第二次读Index block；
  • 第三次读data block；

a. Caching Schemes in LSM-KVS (LSM-KVS中的缓存方案)

如前文所述，在LSM-KVS中有三种类型的条目可以被缓存：KV，KP和Block（如图2所示）。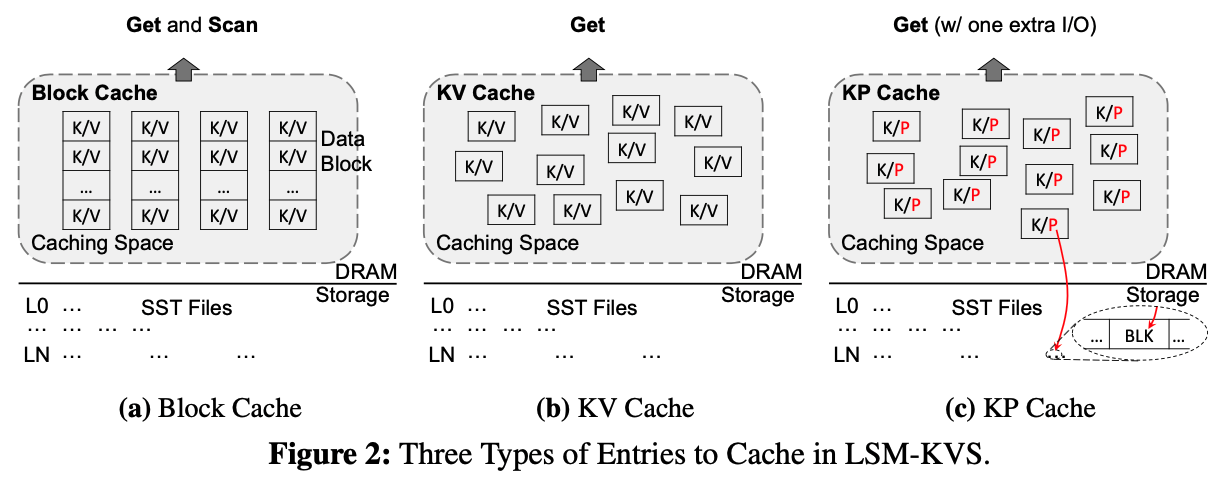
image-20211209162834502

LevelDB仅采用了「Block Cache」（如图2a所示），这里的「Block」可以是：data block，index block，以及Bloom Filter block。「Block Cache」中的「block」使用SST file ID和block offset（例如，<SstID | BlockOffset>）来索引。「Block Cache」可以同时服务「point lookup」和「range query」。虽然Block Cache也能够服务point lookup，但是空间成本太高，因为只有「Block」中的小部分「key-value」才会被频繁访问。
RocksDB同时支持Block Cache和KV Cache（如图2b所示）。KV Cache缓存的KV对可以服务于point lookup。但是RocksDB中Block Cache和KV Cache的缓存大小都是预定义好的，一旦配置完成就无法动态调整。
Cassandra支持KV Cache和KP Cache（如图2c所示），但是不支持Block Cache。在KP Cache中，value在磁盘中的位置作为指针被缓存到内存中。一旦命中了KP Cache，因为KP Cache中已经保存了value在磁盘中的位置，所以仅需要一次额外的磁盘I/O就可以完成「point lookup」。与KV Cache相比，在面临较大的value时，KP Cache以一次额外的磁盘I/O为代价带来了更低的内存空间成本（也即空间效率更高）。但是，与KV Cache相似，KP Cache也不支持「range query」。

b. General Caching Algorithms (通用的缓存算法)

Adaptive Replacement Cache (ARC，自适应替换缓存)是为管理DRAM中的「页缓存」而设计的「动态页面替换算法」。如图3所示，ARC将缓存空间划分为两个部分：「recency cache」 和 「frequency cache」，它们每个都是一个LRU（Least Recently Used，最近最少使用）缓存。 在ARC中，当一个页面第一次被访问时，将会被放到「recency cache」中，如果此页面在被移出「recency cache」前（也即被替换前）得到了第二次访问，则此页面会被认为是一个「frequently accessed page」，然后会将其进一步迁移到「frequency cache」。
recency cache和frequency cache之间的空间分配是动态的。ARC使用两个ghost cache来分别存储从recency cache和frequency cache 中替换出来的页面的元数据。ghost cache中缓存的页面元数据将会作为将来调整各部分缓存空间的参考。与real cache（也即存储完整页面的cache）相比，ghost cache的空间大小几乎可以忽略不计，因为它们只存储页面编号。
recency ghost cache的命中意味着recency cache的缓存空间应该更大，如图3上部所示，目标边界应该向左移动，反之亦然。因此，相应的real cache会根据工作负载来增大或减小。

image-20211209175114565

但是，像ARC这种基于页面的缓存算法都不很适合LSM- KVS，因为它们都基于「页面大小」和「缓存收益」一致的假设。而在LSM- KVS中，不同的key-values的「大小」以及「缓存它们所带来的收益」是不一样的，也即「缓存成本」和「缓存收益」不统一（缓存成本为缓存条目所占用的内存空间，缓存收益为缓存条目所能节省的磁盘I/O次数）。
因此，在LSM-KVS的缓存方案设计中，「缓存成本」和「缓存收益」应该和「访问频率」一块被考虑。

0x20 Motivation

0x21 Unique Challenges in Caching for LSM (面临的挑战)

首先，与页面缓存替换问题相比，页面缓存替换问题中的页面大小是固定的，而LSM树中的key-values大小不是一致的。因此，在LSM中的缓存算法在设计替换算法时，应该将key-values大小的不一致性纳入考虑范围。
此外，LSM-KVS有两种截然不同的读取操作，也即point lookup和range query，对缓存的需求不一致，这也在设计LSM缓存算法时也带来了额外的挑战。
最后，LSM-KVS的Compaction和Flush操作会使缓存的条目失效，在设计缓存方案时也要进行特殊处理。

0x22 What to Cache in LSM-KVS (缓存什么的问题)

将缓存KV和KP进行比较，命中KV能节省更多次数的磁盘I/O，因为命中KP仍然需要一次额外的磁盘I/O操作。但是，另一方面，当value过大时，缓存KP的成本更低，空间利用更高效。
Lesson 1: 应该结合缓存KV和KP条目的优点，来更高效的服务「point lookup」。

但是遗憾的是，缓存KV和KP都不能支持「range query」，因此LevelDB和RocksDB都选择缓存「data block」来为「range query」服务。
Lesson 2: 缓存block或者KV/KP都有它们各自的优势来支持「range query」或「point lookup」。也即每种缓存条目都有其适用的工作负载。

0x23 How to Perform Replacement (如何执行替换的问题)

从上文的讨论可知，每种缓存条目都有其适应的工作负载场景。表1列出了各种缓存条目的比较。但是设计一个由三种缓存条目组成的替换算法是极具挑战的。
image-20211209183758144

现有的成本感知缓存方案（cost-aware caching schemes）并没有针对LSM-KVS的场景做缓存成本和收益的分析。
Lesson 3: 缓存算法应该根据LSM-KVS独特的分层结构，考虑不同缓存条目所「占用DRAM空间大小的不同」，以及「节省的I/O次数的不同」。

通常，现有缓存算法会为各种缓存条目设置固定大小的缓存空间，但这会带来一系列问题。首先，很难设置最优的缓存空间分配；其次，即使一开始设计好了最优的缓存空间分配，但随着工作负载发生变化，之前设置的缓存空间分配便不再适用。
Lesson 4：缓存算法应该能够自适应工作负载的变化。

0x30 Technique: AC-Key Design

AC-Key同时支持缓存三种类型（KV，KP和Block）的条目，并为它们设计了单独的缓存组件。此外，各个缓存组件的空间大小会根据「分层自适应缓存算法」（hierarchical adaptive caching algorithm，HAC）来调整，该算法考虑了不同缓存条目的异构成本和收益，并使用一个「缓存效率因子」（caching efficiency factor）来指导缓存组件大小的调整。

0x31 AC-Key Caching Components

AC-Key的系统架构如图4所示。Block，KP和KV缓存，通过E-LRU进行管理，E-LRU是一种改进的LRU（基于缓存效率因子来选择缓存条目进行逐或者说是替换）。
image-20211209191340705

在一个point lookup中，如果一个lookup-key是首次被访问，则会先将它存到KP Cache中。缓存到KP Cache中的key被称为「warm key」。如果KP Cache中的一个「warm key」被再次命中，我们会将其视为一个「hot key」。我们预计将来访问它的可能性更高。因此，我们会将其提升到KV Cache中，来为将来的访问减少潜在的磁盘I/O次数。
一种优化方式是，如果KV对比KP对还要小，我们会将key-value缓存到KP Cache中，而不是选择将KP缓存到KP Cache中，这样既能避免额外的磁盘I/O，还能节省缓存空间。不过这个KV对仍然需要再次命中后才会被移动到KV Cache中。

a. Get Handling

查询一个Store中存在的Key时（也即point lookup操作）。首先会查询MemTable，因为MemTable中可能存在最新版本的Value。如果没有在MemTable中查询到，则会在KV和KP缓存中查询，将会发生以下情形：

  • Case I：命中KV Cache。不需要磁盘I/O，直接返回相应Value值即可；
  • Case II：没有命中KV Cache，但是命中KP Cache。此时，先检查指针指向的数据块是否被缓存到Block Cache中，如果没有则将此数据块加载到Block Cache中，然后在该数据块中使用二分查找定位KV对。此外，还需要将此Key从KP Cache提升到KV Cache中；
  • Case III：既没有命中KV Cache，也没有命中KP Cache。将会一个Level一个Level的查询每个有序run，查找完成后将其缓存到KP Cache中（需要注意的是，在检索SST时会使用到BF block以及Index block，如果它们不在Block Cache中，也要将它们缓存到Block Cache）；

b. Flush Handling

Flush会将包含最新KV数据的MemTable写入到磁盘组件$L_0$中。需要注意的是，MemTable中的某个Key的旧数据此前可能已经缓存到KV或KP Cache中。如果包含最新数据的MemTable还没有Flush到磁盘上，则在执行Get时会先检查MemTable，KV或KP Cache中的旧数据不会对Get造成影响，但是如果将MemTable Flush到磁盘上，则在执行Get操作时可能得到的是缓存中的旧版本的数据。因此，必须在Flush前完成MemTable和缓存中重叠Key的同步（只要有缓存就有可能存在缓存不一致的问题）。
有两个可以进行同步的时间点，一种是在Put期间同步，一种是在Flush期间同步。
如果在Put期间进行同步，则在每次Put操作时都需要检查缓存中的条目，会带来额外的开销；此外，在此期间无法更新KP Cache，因为MemTable还没写到SST中，无法获得指针。
因此，AC-Key选择仅在Flush时进行同步，这时只需要同步一次，并且可以在此时计算出指针地址来更新KP缓存。

c. Compaction Handling

Compaction操作会影响KP和Block Cache。因为此操作会删除旧的SST，而旧的SST中的数据可能已经缓存到了KP或Block Cache中。需要注意的是此操作不会影响KV Cache，因为Compaction操作不会修改数据，只会进行重排和合并。
AC-Key会更新受到到Compaction影响的KP或Block Cache。

0x32 Caching Efficiency Factor

为了对缓存条目的成本和收益进行定量分析和权衡，本文根据LSM-KVS独特的分层结构提出了一个「缓存效率因子」。使用此缓存效率因子，AC-Key将LRU改进为E-LRU来管理每个缓存组件内部的替换操作。此外，AC-Key还通过这个缓存效率因子将ARC改进为E-ARC来调整各个缓存组件的大小。
本文将一个缓存条目的缓存效率因子$E$（$E$代表Efficiency）定义为如下等式：
image-20211209202701009

其含义是每字节的DRAM空间所节省的I/O次数。
其中，$b$代表如果此条目被缓存，其潜在所能节省的I/O次数，它由如下等式给出：
image-20211209203050655

函数式$f(m)$依赖于LSM-KVS的实现，通常$f(m) = m+2$，也即需要读$m个BF + 1个index\ block + 1个data \ block$ 。
传统的LRU仅考虑了访问模式，而没有考虑缓存条目的收益和成本不同。将LRU与缓存效率因子结合所得的E-LRU便是为了解决这一问题。E-LRU检查最少使用的a个缓存条目，并从中选出缓存效率因子最小的那个条目进行替换。$a$的值取决于缓存条目的缓存效率因子$E$的方差，它由$a= e^{v}$给出，其中$v$是缓存条目的缓存效率因子$E$的标准偏差。
当$v=0$时，所有缓存条目具有相同的缓存效率，此时$a=1$，E-LRU退化为LRU。此外，$a$有一个上限值，以避免在做出替换决定时需要检查过多的条目。

0x33 HAC: Hierarchical Adaptive Caching

Hierarchical Adaptive Caching (HAC)具有两级层次结构来管理不同的缓存（如图5所示）。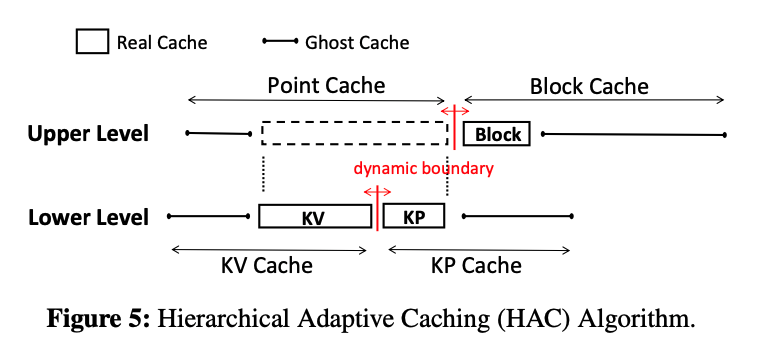
image-20211209211404375

在上层，缓存被分为两个组件：Point Cache以及Block Cache，两个组件之间的边界可以动态调整。
在下层，Point Cache被进一步分为KV Cache 和KP Cache，同样也有一个动态调整的边界。
HAC通过维持ghost caches来保存从KV Cache、KP Cache和Block Cache中替换出来条目的记录。在上层和下层各有两个ghost cache。与ghost cache相对应，原始的KV Cache、KP Cache和Block Cache被称为real cache。在这里，KV Real Cache和KP Real Cache组成Point Real Cache。
ghost cache并不保存真正的条目，只保存相关条目的元数据。一个ghost cache的命中意味着本应该命中对应的real cache的，如果real cache足够大的话。通过使用ghost cache和缓存效率因子，文章设计了E-ARC来调整相应的real cache的大小。

a. Lower-Level HAC

在下层HAC，Point Cache被划分为KV Real Cache($R_{KV}$)和KP Real Cache（$R_{KP}$），这里有
$$
\left | R_{KV} \right |+\left | R_{KP} \right | = \left | S_{point} \right |
$$
其中$\left | S_{point} \right |$表示Point Cache的大小。AC-Key维护KV Ghost Cache，就好像$R_{KV}$ 加上$G_{KV}$的缓存大小就等于整个Point Cache的大小（这是用于暗示$R_{KV}$最大可以扩展到整个Point Cache的大小，而此时相应的$R_{KP}$的大小为0）。因此，在这个前提下，下面的等式成立：
$$
\left | S_{point} \right |=\left | R_{KV} \right |+\left | R_{KP} \right | = \left | R_{KV} \right |+\left | G_{KV} \right |=\left | R_{KP} \right |+\left | G_{KP} \right | \ \ \ Eqn.4
$$
下面展示E- ARC处理缓存命中和未命中的几种情况：

  • Case I：命中Real Cache。缓存命中$R_{KV}$或$R_{KP}$，将该条目移动到$R_{KV}$的MRU端。特殊的，如果命中发生在$R_{KP}$则需要一次额外的磁盘I/O来获取Value，然后将该key-value对提升到$R_{KP}$中。
  • Case II：命中KV Ghost Cache。这意味着$R_{KV}$应该更大，因此向KP Cache方向调整目标边界，调整步幅为$\delta = kE$，$E$代表$G_{KV}$中命中条目的缓存效率因子，$k$是配置的学习率。从磁盘中读完数据后将其插入到$R_{KV}$的MRU端。为了给该条目腾出空间，如果目标边界在$R_{KV}$内部的话，这意味着KV Cache的目标大小比当前大小还要小，不能扩充，只能在KV Cache内部通过E-LRU算法进行替换。
  • Case III：命中KP Ghost Cache。这意味着$R_{KP}$应该更大，因此调整目标边界，同Case II类似。
  • Case III：未命中缓存。此时需要检索磁盘，然后将读取的数据缓按照KP的格式存到$R_{KP}$中。此外，$R_{KP}$同样需要为该条目腾空子，需要根据目标边界的实际情况来确定是调整$R_{KP}$的大小来腾空子还是通过缓存替换来腾空子。

$R_{KV}$和$R_{KP}$之间的目标边界指示着实际边界应该移动的方向，但是需要注意的是，实际边界总是滞后于目标边界的。
高层的操作顺序如下：

  1. 命中ghost cache则调整目标边界；
  2. 需要缓存的条目的插入或提升（从KP Cache提升到KV Cache）使得实际边界向目标边界方向调整，相应的，$R_{KV}$和$R_{KP}$的大小得到更新；
  3. 基于新的Real Cache的大小和Eqn.4（上文的等式4）来调整对应的Ghost Cache的大小；
  4. Real Cache和Ghost Cache在需要适配更新后的大小时通过E-LRU算法来执行替换；

b. Upper-Level HAC

在HAC的上层，我们重新应用E-ARC来调整Point Cache和Block Cache之间的边界。Block Cache和Point Cache各自都有一个 Real Cache和一个Ghost Cache。需要注意的是，从$R_{point}$中替换出来的条目不光要插入到$G_{point}$还要插入到下层的$G_{KV}$或$G_{KP}$中。与下层相似，上层的Cache空间也存在类似的等价关系：
$$
\left | S_{total} \right |=\left | R_{point} \right |+\left | R_{block} \right | = \left | R_{block} \right |+\left | G_{block} \right |=\left | R_{point} \right |+\left | G_{point} \right | \ \ Eqn.5
$$
目标边界的调整：
命中$G_{block}$需要将目标边界从$R_{block}$移向$R_{point}$，移动步幅$\Delta = kE$。相应的，$R_{point}$的目标大小将会减少$\Delta$。在下层，调整量将按照$R_{KV}$和$R_{KP}$的当前目标大小的比率按比例分配。例如，当前$R_{KV}$和$R_{KP}$的目标大小分别为$\left | R_{KV}^* \right |$和$\left | R_{KP}^* \right |$，则它们将按照如下方式进行更新：
$$
\begin{matrix}
\left | R_{KV}^* \right | \leftarrow \left | R_{KV}^* \right | - \Delta \frac{\left | R_{KV}^* \right |}{\left | R_{KV}^* \right | + \left | R_{KP}^* \right |}
\\
\left | R_{KP}^* \right | \leftarrow \left | R_{KP}^* \right | - \Delta \frac{\left | R_{KP}^* \right |}{\left | R_{KV}^* \right | + \left | R_{KP}^* \right |}
\end{matrix}
$$
另一方面，如果命中的是$G_{point}$，则需要将目标边界向$R_{block}$方向移动，移动步幅同样为$\Delta = kE$。需要注意的是，这里的$E$会比命中$G_{block}$时的缓存效率因子更大，因为与缓存Block相比，缓存KV和KP在占用相同空间的情况能节省更多的I/O次数。此外，在HAC的上层命中$G_{point}$则意味着会在下层命中$G_{KV}$或$G_{KP}$，在这种情况下会先调整下层的目标边界，再调整上层的目标边界。

实际边界的调整：
当一个block需要插入到Block Cache中（也即Block Cache潜在需要更大的空间时），而Block Cache的实际大小加上此block的大小比其目标大小要大时，Block Cache不会扩容，只能通过E-LRU算法从Block Cache中选择一个block进行替换。而如果Block Cache的实际大小加上此block的大小要比其目标大小要小时，此时就可以对Block Cache进行扩容了（相对应的Point Cache会收缩缓存空间），扩容后就可以将此block插入到Block Cache。
另一方面，如果Point Cache需要更大的容量，HAC会估计其进行扩容后的大小，然后将该大小与其目标大小进行比较，如果小于其目标大小的话，则可以对其进行扩容，相应的，Block Cache需要通过逐出block来收缩缓存空间以给Point Cache提供空间；如果预估的新的Point Cache的大小要大于其目标大小的话，则不能对其进行扩容，只能通过E-LRU算法在Point Cache内部通过替换来为新的缓存条目腾出空间。

c. Reduce Ghost Cache Size

在ARC算法的设计中，从Real Cache中逐出的页面，其内容会被丢弃，仅需要将page number保存在Ghost Cache中。这里，page number的大小与page content相比是可以忽略不计的。
类似的，在AC-Key中Ghost Block Cache的大小与Real Block Cache的大小相比也是可以忽略的，因为Ghost Block Cache中以<SstID | BlockOffset>形式存储的block handle与Real Block Cache中存储的Block相比也是可以忽略的。但是Ghost KV Cache、Ghost KP Cache以及Ghost Point Cache的大小与其对应的Real Cache相比是无法忽略的，这会带来较大的空间开销。
AC-Key通过两种方式来减少Ghost Cache的空间开销：

  • 首先，AC- Key不使用从KV Cache和KP Cache中逐出来的条目的原始Key，而是使用原始Key的哈希值；
  • 其次，可以在自适应缓存方案已经成功建立了一个在KV Cache、KP Cache和Block Cache之间比较有利的空间分配时关闭掉Ghost Cache，来消除其带来的开销。此外，还可以根据当前缓存组件的命中率来判断是否需要打开Ghost Cache以重新指导空间分配；
上一页
2023-12-18 21:59:30 # 论文 #Key-Value #Store #论文阅读
下一页