Less is More: De-amplifying I/Os for Key-value Stores with a Log-assisted LSM-tree

0x00 Motivation

LSM-Tree的结构决定了其必须要管理大量的小键值对。在实际的工作负载中，大量随机且频繁的KV更新请求会快速破坏LSM的结构。因此，LSM-KV Store必须不断通过Compaction操作来维持KV对的有序性并降低同一Level中不同SSTable之间Key的重叠率。此外，在LSM-Tree中，越深层的Level，Compaction会触发的越频繁。这会给系统带来巨大的计算和IO开销。

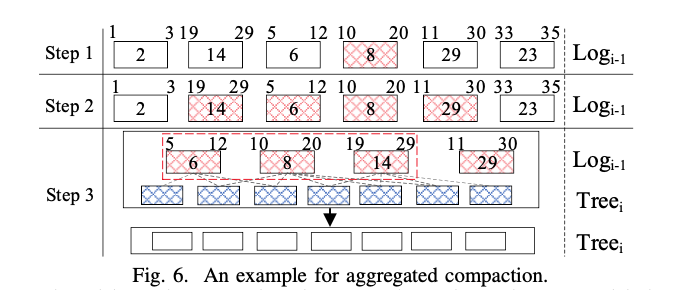
图1展示了LSM-tree的维护成本。上层SSTable的key相较下层较为稀疏，在Compaction操作时会带来很严重的写放大（图中上层的1个SSTable要与下层的4个SSTable执行归并排序，这就意味着下层的4个SSTable都要被重写）。

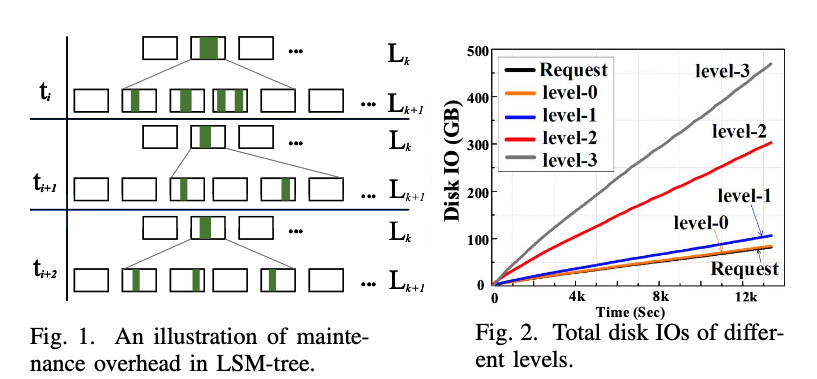
图2展示了随着时间的变化，不同Level的磁盘I/O数量。L0中的SSTable是无序的，因此其维护成本变化不大，其他Level的磁盘I/O都随着请求的增加而增加。此外，可以看到越深层的Level，其磁盘I/O次数增长越快。

0x10 L2SM Design

0x11 Architecture Overview

L2SM的关键设计目标是在维持LSM-Tree结构的基础上，尽量减少I/O放大。

如图3所示，L2SM将数据保存在内存和磁盘中：

• In-Memory structures：与经典LSM-tree结构相似，L2SM维护了两个内存数据结构MemTable和ImmuTable来吸收和组织大量无序且随机的KV对，随后顺序写到磁盘上。
• On-disk structures：磁盘上的数据被划分为两部分，分别存储到LSM-tree和SST-log，SST-log用于吸收那些会破坏LSM-tree结构的操作。SST-log也是个多层结构，除了L0以外，LSM-tree和SST-log层层对应，SST-log也由多个SSTable组成。其目的是用此日志结构来吸收大量对LSM-tree结构造成破坏的操作，以更稳定的状态和更低的更新开销来保护LSM-tree结构。

L2SM的数据流：

1. KV对先写到MemTable中，随后转为ImmuTable，接着Minor Compaction操作会将ImmuTable持久化为L0中的SSTable；
2. 当某一层的SSTable数量达到阈值时，选择出那些对LSM-tree潜在造成较大破坏的SSTable（例如包含hot-key range的SSTable），然后通过Presudo Compaction（PC）操作将其移动到同一Level的SST-log中，由Log Metadata Manager管理。需要注意的是，PC操作只是通过更新元数据来进行逻辑移动，并不会带来任何物理I/O开销。
3. 如果SST-log的Level大小超过阈值，则Aggregate Compaction（AC）操作会从该Level中选择SSTable来与LSM-tree下一Level的有重叠范围SSTable进行合并。

因此，在L2SM中，一个KV项首先会水平从LSM-tree中移到SST-log，然后垂直移动到LSM-Tree的下一Level中。

0x12 LSM-Tree and SST-log

LSM-Tree

在L2SM中，Compaction操作被划分为：PC操作和AC操作。PC操作将SSTable从LSM-Tree移到同一层的SST-Log中，AC操作将SSTable与LSM-Tree中下一Level的重叠SSTable进行合并。

PC和AC操作根据SSTable的属性（hotness和density，热度和密度）来选择SSTable进行移动和合并。

此外，经典LSM-Tree KV-Store一次仅选择一个SSTable来与下一Level的重叠SSTable进行合并。而L2SM一次AC操作会从SST-Log中选择多个SSTable来进行更加密集的合并，以实现更好的I/O性能。

SST-Log

SST-Log主要由以下四个作用：

• 从LSM-Tree中剥离出那些反复破坏LSM-Tree结构的「hot」数据（频繁更新的数据），并将其存到SST-Log提供的独立空间中；
• 提供一个缓冲区来识别和压缩那些键值范围稀疏的SSTable，然后将它们合并到LSM-Tree中；
• 延迟并减轻对LSM-Tree的破坏性操作，例如将多次Compaction操作累积为一个；
• 允许尽早从LSM-Tree中删除过时和lazy delte的数据；

不同于LSM-Tree，SST-Log不要求每一Level中的KV保持有序，因此同一Level的不同SSTable的键值范围会有重叠。所以在SST-Log中进行查找时必须查找所有的SSTable，这会带来一定的开销。但在L2SM中允许这种重叠是必须的，因为SST-Log的设计目的便是为了吸收和累积更新，以使这些更新在AC操作中可以合并为一个，这可以尽量减少对LSM-Tree的影响。

在LSM-Tree中，越深层的Level，其SSTable的访问频率越低，SSTable的密度也更高。因此，对于深层的Level来来说，不需要为其分配太大的SST-Log Level。L2SM通过一个称为「Inverse Proportional Log Size」的方案来决定SST-Log中每一个Level 的大小。具体看原文，这里不多做叙述。

0x13 Hotness and Density

为了减轻对LSM-Tree结构的破坏性干扰，L2SM需要识别出频繁更新和稀疏的SSTable，并将它们隔离在SST-Log中。

L2SM使用两个指标，hotness和density，来定量分析SSTable的属性。「hotness」用于衡量SSTable中KV对的更新频率，「density」用于衡量SSTable的key覆盖和影响的范围。这两个指标共同描述了若将相关KV项保存在LSM-Tree中可能会对LSM-Tree的结构造成潜在破坏的严重程度。

Hotness of SSTables

L2SM通过维护一个「Hotness Detecting Bitmap（HotMap）」来定量分析一个SSTable的「hotness」。HotMap是一个存在于内存中全局多层布隆过滤器（Bloom Filter， BF）。

如图4所示，一个M层的HotMap有M个对齐的BF组成。当一个KV项在第$i$次更行时，将第$i$层的BF相应bit位重置为1。因此，一个M层的HotMap最多可以记录给定KV项的M次更新。

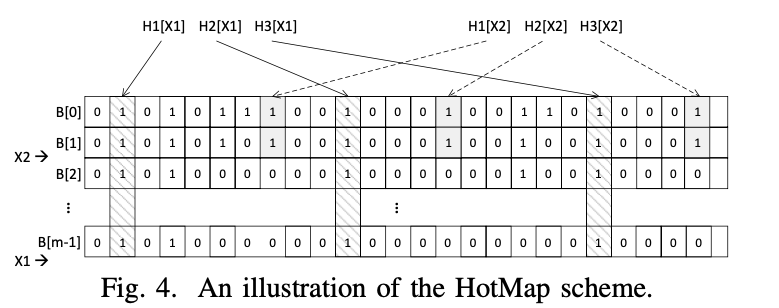
一个SSTable的「hotness」计算方式为$\sum_{i=1}^{m-1}(x_i \times 2^i)$，其中$x^i$表示HotMap指示SSTable中访问次数为$i$的KV项的数量。

HotMap能不能发挥作用主要看参数M和P，下面介绍L2SM是如何配置这两个参数的。

Configuring M

M是HotMap的层数，决定了其能记录的KV项的更新次数。显然M越大，HotMap能记录的更新次数越多，HotMap也就越精确，但这也会带来较大的内存开销。L2SM使用一个简单的方法来设置M。

对$n$个key进行$r$次请求的工作负载，每个key的平均访问次数为$\tau = r/n$，L2SM使用$M = \left \lceil r/n \right \rceil$来设置HotMap的层数。其合理性也很容易解释，当一个KV项的更新次数超过平均更新次数时，该KV项便可以被认为是hot-key。

Configuring P

P是每个BF所表示的bit数组的大小，决定了BF的FPR（False Positive Rate）。当P过小时，BF的FPR会过高，能发挥的作用有限。

另$\rho$表示在工作负载的所有唯一key中hot-key所占的比例。用N表示所有唯一Key的数量，K表示BF中使用的哈希函数数量，根据已有的研究，bit数组的大小应该被设置为$P = \frac{K \times N}{ln2}$。

Auto-turning HotMap

随着时间的推移，HotMap会被逐渐填满，最终失去区分hot-key和cold key的作用。因此，必须确保HotMap能自适应工作负载，在运行时能始终发挥作用。

为了保持一个较低FPR，需要周期性的对HotMap进行更新和扩容。L2SM提出了一个称为Online Adaptive Auto-tuning的方案来自动调整HotMap。

有几种情况会触发该调整方案来调整HotMap。

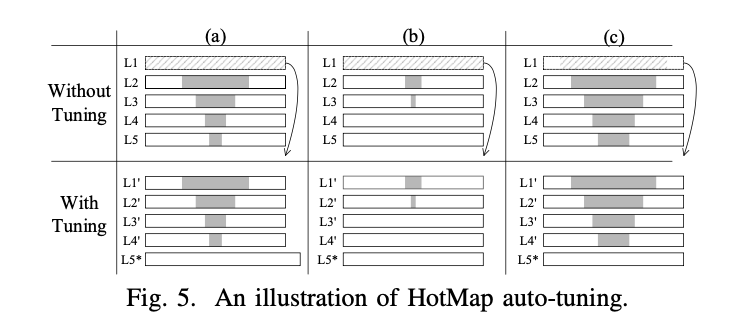
如图5所示，如果顶层的BF接近其容量限制，这表明HotMap过小而无法以较低的FPR来服务于其设计目的，此时将停用该层。当停用该层时，会进一步检查下一层。如果下一层的空间消耗超过20%，则将顶层的BF大小扩大10%，将其所有位重置为0，然后将其旋转到底层，如图5(a)所示；否则，若下一层的使用情况小于20%，为了节省空间，直接将顶层BF的大小设置为当前底层BF的大小，将其所有位重置为0，然后旋转到底层，如图5(b)所示。其原理是，若第二层消耗很小，则很可能大多数键都是冷的，并且工作集没有增长，当前的HotMap大小是足够的。

假设顶层的BF足够大，可以容纳所有的唯一写入，如果任何两个相邻层接受的唯一键太接近（例如，两层之间接受的插入差异小于10%，并且每层占用超过层大小20%），也即两层过于相似，这发生在重复更新一组键时。此时，可以通过重置顶层BF并将其旋转到底层来将其退休，如图5(c)所示。

Overhead

内存开销可以用$M \times P$来表示。M是BF的数量，P是BF的大小。

Density of SSTables

在L2SM中，大多数情况下SSTable的大小一致，并且其KV项是有序的。L2SM使用SSTable中KV项的数量和key range的比值来表示其密度。

SSTable的key range是SSTable中第一个key和最后一个key之间的差。但由于实际工作负载中，key的表示形式不同，可能为字符串或数字。因此不能直接通过数字减法来计算。

L2SM通过将key转换为128位的二进制值来简化此计算过程。然后通过逐位比较两个128位二进制值（比较第一个key和最后一个key），以找到两个key中不同的最高位。假设不同的最高位是第$i$位，则SSTable的key range可以粗算为$2^i$。如果此SSTable包含$k$个KV项，则其密度可以计算为$k/2^i$。为了进一步简化计算，L2SM使用对数来表示SSTable的密度值，即$lg(k/2^i) = lgk - i$。此外，还可以用$S = i - lgk$来表示SSTable的sparseness，这是与density相反的表示方式。

0x14 Pseudo Compaction

在L2SM中，当LSM-Tree中的某个Level被写满时，根据SSTable的hotness 和density ，PC能够快速选择出那些对LSM-Tree结构造成潜在破坏的SSTable，将其隔离在SST-Log中，以降低I/O放大。

为了确定移入SST-Log的最佳SSTable，L2SM使用一个Combined Weight来联合考虑hotness和density，以确定SSTable的选择。

对于给定的SSTable $i$，假设其hotness为$H_i$，sparseness 为$S_i$，则权重方程为$W_i = \alpha \times H_i + (1 - \alpha) \times S_i$，其中$\alpha$

是预设的权重参数，默认为0.5 。

要计算SSTable的组合权重，首先需要将S和H都归一化到0～1之间。归一化后其组合权重可以表示为：
$$
W_i = \alpha \times \frac{H_i}{H_{max} - H_{min}} + (1 - \alpha) \times \frac{S_i}{S_{max} - S_{min}}
$$

0x15 Aggregated Compaction

AC操作负责回收SST-Log的空间，它尝试在SST-Log中保留那些对LSM-Tree结构影响最大的SSTable，并将

冷而密集的SSTable合并到LSM-Tree的下一Level中。

当SST-Log超过其大小限制时，会触发AC操作将冷而密集的SSTable合并到LSM-Tree，同时将热而稀疏的SSTable保存在SST-Log。此时需要对SST-Log中的所有SSTable进行组合权重计算，以选择SSTable。

整个Compaction过程如下所示：

1. 根据组合权重W找到最冷最密集的「种子」SSTable，并使用该SSTable在SST-Log中递归找到所有与它的key range重叠的SSTable，根据版本顺序对所有的SSTable进行排序；
2. 基于步骤1选择出的SSTable，从最旧的SSTable开始，放入victim Compaction Set（CS），在LSM-Tree的下一Level中找到与CS中的SSTable有重叠Key range的SSTable，将其放入victim Involved Set（IS）；
3. 重复步骤2，直到步骤1中找到的所有SSTable都放在CS中，或者IS和CS中SSTable的比值大于预设值（默认为10，用于控制AC所引起的I/O放大）；
4. 最后开始正式的归并排序。首先从CS中最旧的SSTable开始，删除其中所有已标记删除和过时的KV项。然后将其与IS中的相关SSTable进行合并，最后将生成的新的SSTable插入到LSM-Tree的下一Level中，这样便完成了AC过程。

图6是该AC过程的一个示例。块中的数字表示其时间顺序，也即版本（越小表示越旧）。SST-Log中有6个SSTable，SSTable 8为最冷最密集的SSTable，有三个SSTable与其有重叠（SSTable 6、14和29）。CS中包括SSTable 6、8和14，虽然SSTable 29也与SSTable 8有重叠，但因为超过了I/O限制，其不参与此次AC过程。所以，最后是SSTable 6、8和14与IS中的SSTable进行合并重写。