「TriangleKV」论文阅读。
2023-12-18 22:00:08 # 论文 #Key-Value #Store #论文阅读

TriangleKV

  • 论文名称：TriangleKV_Reducing_Write_Stalls_and_Write_Amplification_in_LSM-tree_Based_KV_Stores_with_Triangle_Container_in_NVM
  • 期刊：TPDS
  • 时间：2022

Introduction

为了更好的理解基于LSM的KV存储，论文对传统使用DRAM-SSD的RocksDB进行了实验评估，发现了两个具有挑战性的问题，及其根本原因：

  • 写停滞（write stalls）会导致应用程序的吞吐量周期性的骤降到接近为0，从而会导致性能的剧烈波动和长尾延迟。论文的研究表明，导致写停滞的主要原因是L0-L1之间Compaction的数据量过大，发生L0-L1之间的Compaction时，几乎涉及到这两个Level的所有数据（L0的数据是无序的，SSTable之间有Key Range的重叠）。
  • 写放大（write amplification，WA）会降低系统的性能和存储设备的耐用性。写放大与LSM-Tree的深度直接相关，更大的数据集会产生更深的LSM-Tree，从而增加Compaction的数量。
    已有的大量研究都局限于解决上述的单个问题，而本篇论文的研究旨在同时解决这两个挑战。
    针对这两个挑战和其根本原因，本篇论文提出了TriangleKV，一个使用DRAM-NVM-SSD混合存储设备的LSM-Tree KV存储。
    TriangleKV的设计原则包括：
  • 利用NVM来为L0和L1提供代价更低，更细粒度的Compaction操作；
  • 减少LSM-Tree的深度以减少写放大；

Background and Motivation

NVM是一种按字节寻址，持久化的快速存储设备。它有望以更低的成本提供类似DRAM的性能、磁盘的持久性和比DRAM更高的容量。和SSD相比，NVM有望提供100倍的低读写延迟和10倍的高带宽。
NVM既可以作为通过PCIe接口访问的持久化块存储设备，也可以作为通过内存总线访问的主存。现有的研究表明，第一种使用方式只能实现边缘性能的提高，浪费了NVM的高介质性能；对于第二种方式来说，NVM可以替代或者作为DRAM的补充，比如作为一个单级内存系统、一个NVM-SSD混合系统或一个DRAM-NVM-SSD混合系统。
基于以下原因，具有DRAM-NVM-SSD的混合存储系统被认为是利用NVM的最高效方式：

  • NVM在未来几年有望与大容量SSD共存；
  • 与DRAM相比，NVM仍然有低5倍的带宽和高3倍的读延迟；
  • 混合系统平衡了TCP（Total Cost of Ownership）和系统性能；
    因此，TriangleKV旨在具有DRAM、NVM和SSD的混合存储系统中更有效的使用NVM作为持久存储。

写停滞（Write Stalls）

在基于LSM的KV存储中，存在三种类型的「停滞」：

  • 插入停滞（Insert Stalls）：如果MemTable在后台完成刷新操作之前写满了，所有的插入操作都会停滞；
  • 刷新停滞（Flush Stalls）：如果L0中的SSTable数量达到上限，后台刷新操作就会被阻塞；
  • 压缩停滞（Compaction Stalls）：挂起的Compaction操作太多会阻塞前台操作；
    这三种停滞都会对写性能造成影响，并导致写停滞。

NoveLSM

如图1(a)所示，NoveLSM利用NVM为具有DRAM-NVM-SSD的系统提供高吞吐量。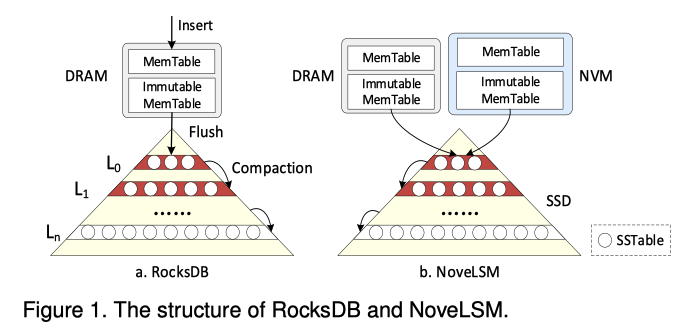
Untitled

NoveLSM的设计选择包括：

  • 采用NVMs作为DRAM的备选来增加MemTable和 immutable MemTable的大小；
  • 使NVM中的MemTable可变，允许直接更新，从而减少Compaction的次数；
    但是这些设计选择仅仅只是推迟了「写停滞」。当数据集的大小超过NVM MemTable的容量时，「刷新停滞」还是会发生，并阻塞前台的请求。
    此外，当NVM中扩大的MemTable刷新到L0，会显著增加L0-L1的Compaction中的数据量，这会导致更长的Compaction延迟和更严重的写停滞（如图4所示）。

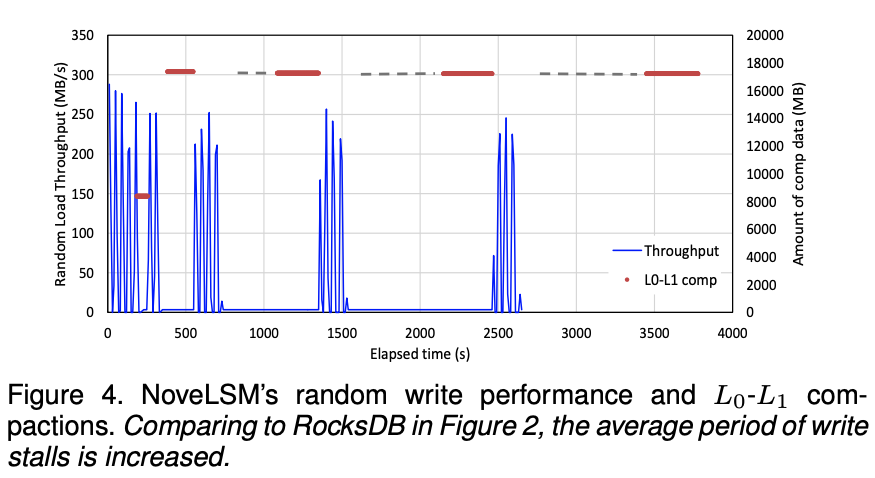
Untitled

通过以上分析可以得出，L0-L1之间的Compaction中涉及的大量数据是导致「写停滞」的主要原因，而「写放大」增加的主要原因是LSM-Tree深度的加深。「写停滞」和「写放大」的综合影响会降低系统吞吐量，并延长尾延迟。

MatrixKV

如图5所示，MatrixKV仍然使用DRAM来管理MemTable和ImmMemTable，但是使用NVM来管理WAL。没有将MemTable和ImmMemTable放在NVM是因为：

  • 与DRAM相比，NVM仍然有5倍高的低带宽和3倍高的读延迟，使用NVM可能会降低读写性能；
  • 往MemTable中插入数据需要查询「跳表」，并且会涉及到多个指针的修改，这些操作对于NVM来说开销也是昂贵的；

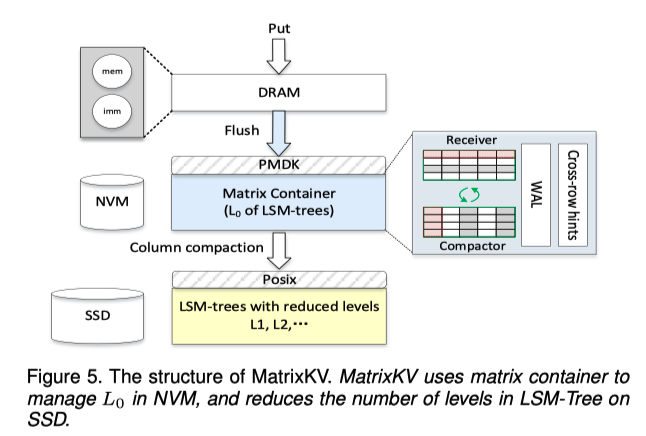
Untitled

此外，MatrixKV还将L0移动到NVM中，将L0放在NVM中有以下优势：

  • 与SSD相比，NVM有更高的带宽和更低的延迟，因此在将ImmMemTable刷新到L0中时会更快，这会减少「插入停滞」；此外，这还隔离了L0-L1的Compaction操作和刷新操作之间的交互，此时两者之间没有带宽的竞争，从而能减少写停滞；
  • NVM是字节寻址的，这意味着L0-L1的Compaction可以在非常细的粒度上完成，并且在每次细粒度Compaction之后可以立即释放空间，而将L0放在SSD上不能实现这一点，因为SSD上的SSTable在整个文件压缩之前不能被删除；

MatrixKV使用「矩阵容器」来管理L0，其中包括一个「接收器（Receiver）」和一个「压缩器（Compactor）」。不可变的MemTable首先被「刷新」到「接收器」，当「接收器」达到其大小限制时，它被转换为「压缩器」，并生成一个新的「接收器」来接受「刷新」操作。
通过一个「细粒度列压缩（Column Compaction）」，「压缩器」中的数据被Compacted到SSD上的L1中。每次只Compact特定键范围内的一小部分数据，这大大减少了「写停滞」。

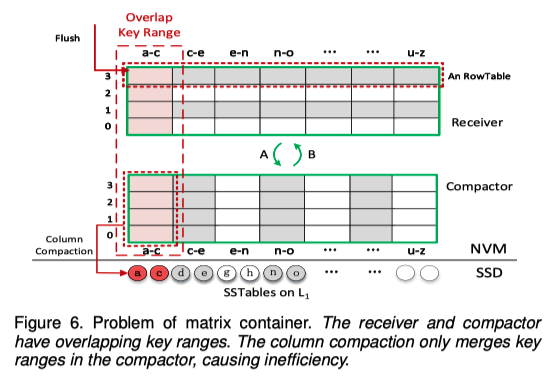
Untitled

但是列压缩只能对「压缩器」使用，「接收器」中与「压缩器」重叠的键范围并不能参与「列压缩」过程。
如图6所示，「压缩器」中的a-c键范围首先通过「列压缩」被Compact到L1，而「接收器」中与其重叠的键范围仍然在L0中。当「接收器」转变为「压缩器」后，这些键范围需要被再次执行Compact操作，这意味着在L1中写入了两次键范围为a-c的数据，带来了额外的「写放大」。

TriangleKV Design

TriangleKV 在MatrixKV的基础上进行了改进，将后者的Matrix数据结构替换为Triangle数据结构，来对L0进行更有效的管理。
图7展示了TriangleKV的架构，从上到下依次为：

  • DRAM，用于批量写MemTable；
  • MemTable刷新到L0，并由NVM中的「三角形容器」（Triangle Container）来存储和管理；
  • L0中的数据通过「直角边压缩」（right-angle side compaction）压缩到SSD中的L1层；
  • SSD中存储一个扁平化的LSM-Tree的剩余Level；

TriangleKV Container

L0-L1的Compaction所带来的大量I/O被认为是导致「写停滞」的根本原因。因此，基于LSM-Tree的KV存储，最小化或者消除「写停滞」的设计原则就是降低L0和L1的Compaction粒度以及减少SSD上的I/O次数。
基于以上设计原则，TriangleKV将L0从SSD移动到NVM，并将L0组织为一个「三角形容器」，以利用NVM的可字节寻址和高速随机访问能力。所谓的「三角形容器」是L0的一种数据管理结构（图8展示了其组织结构）。

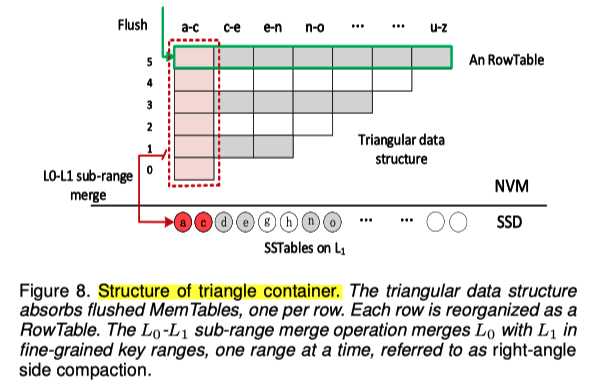
Untitled

三角形数据结构：

在三角形容器中，从DRAM刷新下来的ImmMemTable按「row」堆在NVM中。每一个这样的MemTable根据其键范围被重组为一个RowTable。RowTable作为三角形的底边不断堆叠增加，也即从0到n。三角形数据结构的大小从一个RowTable开始，当三角形数据结构达到其大小上限时（例如NVM容量的60%），会触发一个L0-L1的「子范围合并」操作。
参与「子范围合并」合并操作的是三角形数据结构的「垂直直角边的数据」，也即最长时间未被合并的子键值范围数据。
L0-L1的子范围合并操作与DRAM的刷新操作是同步执行的，因此NVM中的数据结构保持在三角平衡状态。

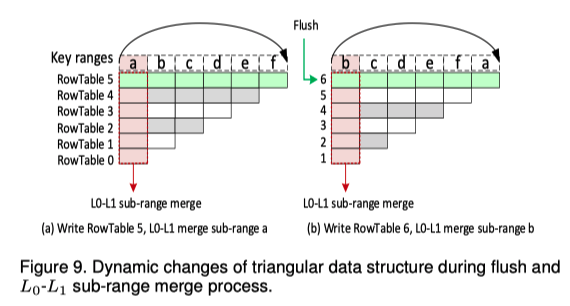
Untitled

图9展示了在刷新和L0-L1子范围合并过程中三角形数据结构的动态变化示例。
在图9(a)中共有9个RowTable，序号从0到5。假设总键值空间为a-f，则参与合并的子键值范围为a。完成子范围a的L0-L1合并后，所有属于此范围的数据都被写到SSD中，此时NVM中的每个RowTable都不再包含属于键值范围a的数据。
如图9(b)所示，当DRAM刷新另一个ImmMemTable时，一个RowTable 6被添加到NVM的三角形数据结构中，RowTable 6的键值范围为a-f，此时只有RowTable 6包含键值范围a。L0-L1子范围合并被旋转到键值范围b，这样每个RowTable中属于键值范围b的数据都会被合并到L1层。
如图9所示，在L0-L1的不断子范围合并过程中，RowTable从DRAM刷新到NVM，并不断地向三角形数据结构的底部增加新的RowTable。始终选择最长时间未参与子范围合并的子键范围进行合并，并将新添加的RowTable相关子范围旋转到后面，如图9(a)所示，将未参与子范围a合并的RowTable 5的范围a旋转到了尾部。这会构成一个「动态三角形」，也即「三角形数据结构」的名称来源。

RowTable：
图10(a)展示了RowTable的结构组成：数据区域和元数据区域。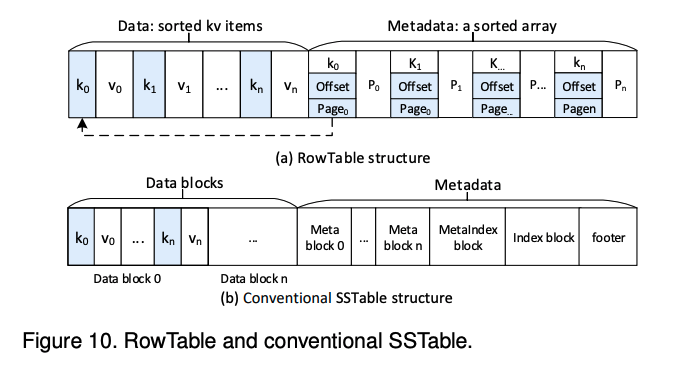
Untitled

为了构造一个RowTable，首先将ImmMemTable中的KV项按照键顺序序列化，并将其存储在数据区域。然后用一个排序数组构建所有KV项的元数据。每个数组元素维护「键」、「页编号」、「页内偏移量」和一个「前向指针」。
为了定位RowTable中的一个KV项，对有序元数据数组执行二分查找，以获取Key，并通过页编号和页偏移量获取Key对应的Value。每个数组元素中的前向指针用于「跨行提示搜索」，这有助于提高三角形容器内的读取效率。
图10(b)展示了一个传统LSM-Tree SSTable的结构。SSTable是使用SSD和HDD的存储单元以「块」为基本单元进行组织的。而RowTable使用NVM中的「页」作为它的基本单元。

L0-L1 sub-range merge：
「三角形容器」的一个主要作用就是从L0中选择数据并合并到NVM上的L1中去。利用NVM的可字节寻址能力，以及前面所提出的RowTable，TriangleKV允许L0中的指定子键范围与L1中SSTable的子集进行合并，实现了更低代价的Compaction操作，而不需要合并整个的L0和L1。
这种新的L0-L1合并方式被称为「直角边压缩」。
在「三角形容器」中，KV项采用逻辑三角形数据结构进行管理。三角形数据结构的「直角边」是具有有限数据量的键空间的子集，它是三角形容器中「直角边压缩」的基本单元。
具体来说，来自不同RowTable的属于「直角边压缩」键范围的的KV项在逻辑上构成直角边。这些KV项的数量是直角边的大小，这个大小不是严格固定的，而是受「直角边压缩」大小的阈值所决定的。

Space management：
完成「直角边压缩」后，「直角边」所占用的NVM空间会被释放。为了管理这些空闲空间，TriangleKV应用了「分页算法」。
「直角边压缩」后释放的空闲页作为一组页单元加入到一个「空闲列表」中。然后将使用「空闲列表」中的空闲页来存储从DRAM刷新得到RowTable。
8GB大小的「三角形容器」包含$2^{11}$个4KB大小的页。每个页由一个unsigned integer作为页编号来标识。为每个列表元素添加一个8字节的指针，因此列表中每个页的元数据大小为12字节。
空间管理的元数据包含一个「空闲列表」以及一个将RowTable 编号映射到对应元数据页的「数组列表」，在NVM中总共只占用24KB的空间。

Right-angle Side Compaction

「直角边压缩」是一种细粒度的L0-L1压缩，每次只压缩直角边，也即特定键范围内数据的一个子集。因此「直角边压缩」能显著减少「写停滞」。
「直角边压缩」的主要工作过程可以描述为以下七步：

  1. TriangleKV将L1的键空间划分为多个连续的键范围。由于L1中的SSTable是有序的，且每个SSTable都有一个最大和最小Key，L1中所有SSTable的最大和最小Key组成一个有序的Key列表。每两个相邻的Key组成一个键范围，由此得到L1中的多个连续键范围。
  2. 「直角边压缩」从L1的第一个键范围开始。它选择L1中的一个键范围作为压缩键范围。
  3. 在三角形容器中，压缩键范围内的KV项从多个RowTable中并发选取；
  4. 如果当前「直角边压缩」的键范围内的数据量小于压缩的下限，则将L1中的下一个键范围也加入压缩过程，这个键范围扩展过程持续到参与压缩的键范围内的数据量处于压缩下限和压缩上限之间。这个边界保证了压缩过程的适当开销。
  5. 在压缩键范围内的N个RowTable中的KV项组成一条逻辑直角边。
  6. 直角边中的数据和L1中SSTable重叠数据在内存中进行合并排序；
  7. 合并排序后生成的SSTable被写回SSD中的L1。

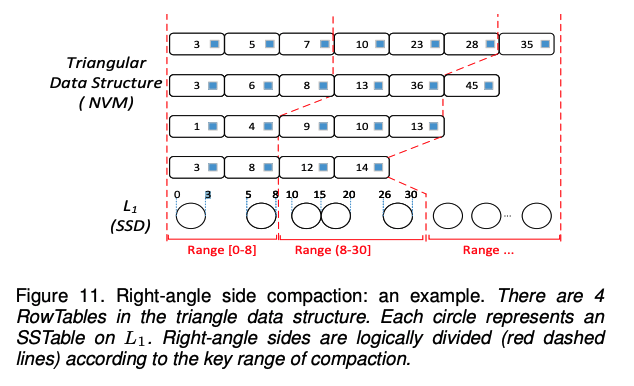
Untitled

图10展示了一个「直角边压缩」的例子。

  • 首先，TriangleKV从L1中选择具有键范围0-3的SSTable作为参与压缩过程的候选SSTable；
  • 然后，查询「三角形容器」中4个RowTable的元数据数组，如果键范围0-3内的数据量小于压缩下限，则下一个邻接键范围也加入压缩，构成一个更大的键范围0-5，如果此键范围内的数据还小于压缩下限则键范围5-8内的数据也加入压缩，键范围扩大到0-8。
  • 最后，一旦键范围内的数据查过压缩下限，便构成了压缩过程的一个逻辑直角边。键范围0-8所组成的逻辑直角边与SSD上L1中的前两个SSTable进行合并。

Reducing LSM-tree Depth

LSM-Tree中Level的数量随着数据库中数据量的增加而增加。而将SSTable压缩到更高的Level会带来AF（Amplification Factor）级别的的写放大，因此总体WA会随着LSM-Tree深度的增加而增加。
因此TriangleKV的另一个设计原则是减小LSM-Tree的深度来缓解写放大。TriangleKV增加每一Level的大小限制，使相邻的AF保持不变，从而减少了LSM-Tree的深度。
因此，对于L1及以上级别的Compaction操作，SSTable到下一Level的压缩WA保持不变，但由于Level的减少，整体的写放大会减少。
使传统的LSM-Tree扁平化会带来两个负面影响：

  • 首先，放大L0后会有更多的SSTable与L0有范围重叠，这增加了参与L0-L1压缩的数据量，这不仅增加了压缩开销，而且延长了「写停滞」的持续时间。
  • 其次，当遍历一个更大的未排序的L0时，搜索效率会降低；

TriangleKV不存在第一个问题，因为「直角边压缩」使L0-L1压缩始终处于细粒度。「直角边」所涉及的数据量在很大程度上与水平宽度无关，因为直角边所包含的数据量是有限的。唯一的缺点是，搜索较大的L0的效率比较低，这可能会降低读取效率。

为了提高「三角形容器」内的读效率，TriangleKV构建了一个「跨行提示搜索」。
Constructing cross-row hints：
当在「三角形容器」中构建一个RowTable时，为有序元数据数组中的每个元素添加一个前向指针（如图10）。具体来说，对于RowTable i中的键x，其前向指针指向前面RowTable i-1中的键y，键y 是第一个不小于x的键，也即y≥x 。
这些前向指针提供了对于不同行的所有键进行逻辑排序的提示。由于每个前向指针只记录前一个RowTable的数组索引，所以前向指针的大小只有4字节，因此存储开销非常小。

Search process in the triangle container：
查询过程从最后到达的RowTable i开始。如果该RowTable的键范围并没有覆盖目标键，则跳到它的前一个RowTable，也即RowTable i-1；如果覆盖了目标键，则在RowTable i中执行二分查找，以找到目标键所在的键范围。
使用前向指针可以缩小前面RowTable中的搜索区域。因此，不需要完全遍历所有表来获得一个键或扫描一个键范围。跨行提示搜索通过显著减少搜索过程中涉及的表和元素的数量，提高了L0的读取效率。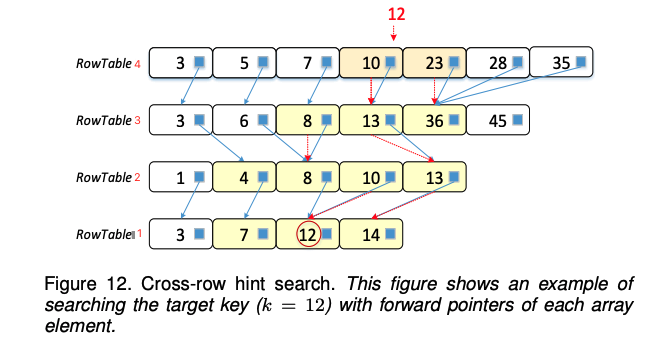
Untitled

图12展示了一个跨行提示搜索的例子。其中蓝色箭头表示前向指针所提供的跨行提示。
假设我们想在三角形容器中查找一个目标键k=12 。

  • 首先对RowTable 1执行二分查找，得到一个缩小的从key=10到key=23的键范围。
  • 通过它们的前向指针提示，查找到RowTable 3中的键13和键36。当目标键不在两个提示键的键范围内时，将上述键添加到搜索区域。
  • 接下来，在key=8和key=36之间执行二分查找，如果找不到目标键，就根据前向指针的提示查找RowTable 2，然后是查找RowTable 1，最后在RowTable 1中查找到键12 。
上一页
2023-12-18 22:00:08 # 论文 #Key-Value #Store #论文阅读
下一页